Warning: This document is for an old version of sdcflows. The main version is master.

sdcflows.workflows.fit.fieldmap module

Processing phase-difference and directly measured \(B_0\) maps.

Theory

The displacement suffered by every voxel along the phase-encoding (PE) direction can be derived from Eq. (2) of [Hutton2002]:

\[\Delta_\text{PE} (i, j, k) = \gamma \cdot \Delta B_0 (i, j, k) \cdot T_\text{ro}, \label{eq:fieldmap-1}\tag{1}\]

where \(\Delta_\text{PE} (i, j, k)\) is the voxel-shift map (VSM) along the PE direction, \(\gamma\) is the gyromagnetic ratio of the H proton in Hz/T (\(\gamma = 42.576 \cdot 10^6 \, \text{Hz} \cdot \text{T}^\text{-1}\)), \(\Delta B_0 (i, j, k)\) is the fieldmap variation in T (Tesla), and \(T_\text{ro}\) is the readout time of one slice of the EPI dataset we want to correct for distortions.

Let \(V\) represent the «fieldmap in Hz» (or equivalently, «voxel-shift-velocity map» as Hz are equivalent to voxels/s), with \(V(i,j,k) = \gamma \cdot \Delta B_0 (i, j, k)\), then, introducing the voxel zoom along the phase-encoding direction, \(s_\text{PE}\), we obtain the nonzero component of the associated displacements field \(\Delta D_\text{PE} (i, j, k)\) that unwarps the target EPI dataset:

\[\Delta D_\text{PE} (i, j, k) = V(i, j, k) \cdot T_\text{ro} \cdot s_\text{PE}. \label{eq:fieldmap-2}\tag{2}\]

Direct B0 mapping sequences

Some MR schemes such as SEI can directly reconstruct an estimate of the fieldmap in Hz, \(V(i,j,k)\). These fieldmaps are described with more detail here.

This corresponds to this section of the BIDS specification.

Phase-difference B0 estimation

The fieldmap variation in T, \(\Delta B_0 (i, j, k)\), that is necessary to obtain \(\Delta_\text{PE} (i, j, k)\) in Eq. \(\eqref{eq:fieldmap-1}\) can be calculated from two subsequient GRE echoes, via eq. (1) of [Hutton2002]:

\[\Delta B_0 (i, j, k) = \frac{\Delta \Theta (i, j, k)}{2\pi \cdot \gamma \, \Delta\text{TE}}, \label{eq:fieldmap-3}\tag{3}\]

where \(\Delta \Theta (i, j, k)\) is the phase-difference map in radians, and \(\Delta\text{TE}\) is the elapsed time between the two GRE echoes.

For simplicity, the «voxel-shift-velocity map» \(V(i,j,k)\), which we can introduce in Eq. \(\eqref{eq:fieldmap-2}\) to directly obtain the displacements field, can be obtained as:

\[V(i, j, k) = \frac{\Delta \Theta (i, j, k)}{2\pi \cdot \Delta\text{TE}}. \label{eq:fieldmap-4}\tag{4}\]

This calculation is further complicated by the fact that \(\Theta_i\) (and therefore, \(\Delta \Theta\)) are clipped (or wrapped) within the range \([0 \dotsb 2\pi )\). It is necessary to find the integer number of offsets that make a region continuously smooth with its neighbors (phase-unwrapping, [Jenkinson2003]).

This corresponds to this section of the BIDS specification. Some scanners produce one phasediff map, where the drift between the two echos has already been calculated (see the corresponding section of BIDS).

References

Hutton2002(1,2)

Hutton et al., Image Distortion Correction in fMRI: A Quantitative Evaluation, NeuroImage 16(1):217-240, 2002. doi:10.1006/nimg.2001.1054.

Jenkinson2003(1,2)

Jenkinson, M. (2003) Fast, automated, N-dimensional phase-unwrapping algorithm. MRM 49(1):193-197. doi:10.1002/mrm.10354.

sdcflows.workflows.fit.fieldmap.init_fmap_wf(omp_nthreads=1, sloppy=False, debug=False, mode='phasediff', name='fmap_wf')[source]

Estimate the fieldmap based on a field-mapping MRI acquisition.

Estimates the fieldmap using either one phase-difference map or image and one or more magnitude images corresponding to two or more GRE acquisitions.

When we have a sequence that directly measures the fieldmap, we just need to mask it (using the corresponding magnitude image) to remove the noise in the surrounding air region, and ensure that units are Hz.

Workflow Graph
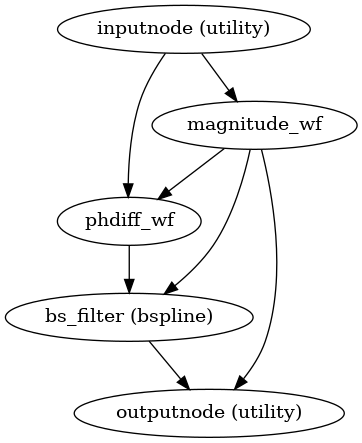
../_images/sdcflows-workflows-fit-fieldmap-1.png

(Source code, png, svg, pdf)

Parameters

  • omp_nthreads (int) – Maximum number of threads an individual process may use.

  • sloppy (bool) – Whether a fast but less accurate correction should be applied.

  • debug (bool) – Run in debug mode

  • name (str) – Unique name of this workflow.

Inputs

  • magnitude (list of str) – Path to the corresponding magnitude image for anatomical reference.

  • fieldmap (list of tuple`(:obj:`str, dict)) – Path to the fieldmap acquisition (*_fieldmap.nii[.gz] of BIDS).

Outputs

  • fmap (str) – Path to the estimated fieldmap.

  • fmap_ref (str) – Path to a preprocessed magnitude image reference.

  • fmap_coeff (str or list of str) – The path(s) of the B-Spline coefficients supporting the fieldmap.

  • fmap_mask (str) – Path to a binary brain mask corresponding to the fmap and fmap_ref pair.

  • method (str) – Short description of the estimation method that was run.

sdcflows.workflows.fit.fieldmap.init_magnitude_wf(omp_nthreads, name='magnitude_wf')[source]

Prepare the magnitude part of GRE fieldmaps.

Average (if not done already) the magnitude part of the GRE images, run N4 to correct for B1 field nonuniformity, and skull-strip the preprocessed magnitude.

Workflow Graph
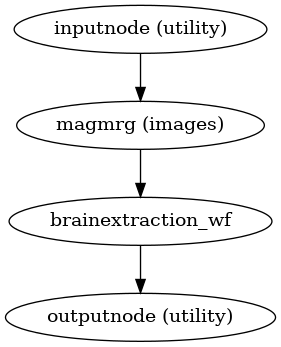
../_images/sdcflows-workflows-fit-fieldmap-2.png

(Source code, png, svg, pdf)

Parameters

  • omp_nthreads (int) – Maximum number of threads an individual process may use

  • name (str) – Name of workflow (default: magnitude_wf)

Inputs

magnitude (os.PathLike) – Path to the corresponding magnitude path(s).

Outputs

  • fmap_ref (os.PathLike) – Path to the fieldmap reference calculated in this workflow.

  • fmap_mask (os.PathLike) – Path to a binary brain mask corresponding to the reference above.

sdcflows.workflows.fit.fieldmap.init_phdiff_wf(omp_nthreads, debug=False, name='phdiff_wf')[source]

Generate a \(B_0\) field from consecutive-phases and phase-difference maps.

This workflow preprocess phase-difference maps (or generates the phase-difference map should two phase1/phase2 be provided at the input), and generates an image equivalent to BIDS’s fieldmap that can be processed with the general fieldmap workflow.

Besides phase2 - phase1 subtraction, the core of this particular workflow relies in the phase-unwrapping with FSL PRELUDE [Jenkinson2003]. FSL PRELUDE takes wrapped maps in the range 0 to 6.28, as per the user guide.

For the phase-difference maps, recentering back to \([-\pi \dotsb \pi )\) is necessary. After some massaging and with the scaling of the echo separation factor \(\Delta \text{TE}\), the phase-difference maps are converted into an actual \(B_0\) map in Hz units.

Workflow Graph
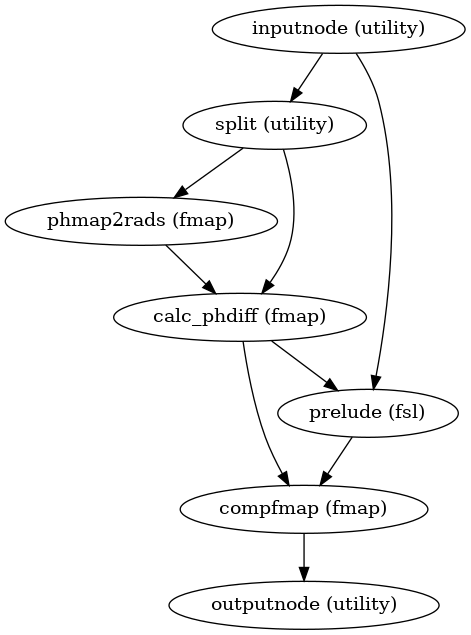
../_images/sdcflows-workflows-fit-fieldmap-3.png

(Source code, png, svg, pdf)

Parameters

  • omp_nthreads (int) – Maximum number of threads an individual process may use

  • debug (bool) – Run in debug mode

  • name (str) – Name of workflow (default: phdiff_wf)

Inputs

  • magnitude (os.PathLike) – A reference magnitude image preprocessed elsewhere.

  • phase (list of tuple of (os.PathLike, dict)) – List containing one GRE phase-difference map with its corresponding metadata (requires EchoTime1 and EchoTime2), or the phase maps for the two subsequent echoes, with their metadata (requires EchoTime).

  • mask (os.PathLike) – A brain mask calculated from the magnitude image.

Outputs

fieldmap (os.PathLike) – The estimated fieldmap in Hz.