Susceptibility Distortions in a nutshell¶
This notebook is an attempt to produce educational materials that would help an MRI beginner understand the problem of SD(C).
[1]:
%matplotlib inline
[2]:
import matplotlib as mpl
from matplotlib import pyplot as plt
from mpl_toolkits.axes_grid1.inset_locator import inset_axes
plt.rcParams["figure.figsize"] = (12, 9)
plt.rcParams["xtick.bottom"] = False
plt.rcParams["xtick.labelbottom"] = False
plt.rcParams["ytick.left"] = False
plt.rcParams["ytick.labelleft"] = False
Some tools we will need:
[3]:
from itertools import product
import numpy as np
from scipy import ndimage as ndi
import nibabel as nb
from templateflow.api import get
[4]:
def get_centers(brain_slice):
samples_x = np.arange(6, brain_slice.shape[1] - 3, step=12).astype(int)
samples_y = np.arange(6, brain_slice.shape[0] - 3, step=12).astype(int)
return zip(*product(samples_x, samples_y))
def plot_brain(brain_slice, brain_cmap="RdPu_r", grid=False, voxel_centers_c=None):
fig, ax = plt.subplots()
# Plot image
ax.imshow(brain_slice, cmap=brain_cmap, origin="lower");
# Generate focus axes
axins = inset_axes(
ax,
width="200%",
height="100%",
bbox_to_anchor=(1, .6, .5, .4),
bbox_transform=ax.transAxes,
loc=2,
)
axins.set_aspect("auto")
# sub region of the original image
x1, x2 = (np.array((0, 48)) + (z_s.shape[1] - 1) * 0.5).astype(int)
y1, y2 = np.round(np.array((-15, 15)) + (z_s.shape[0] - 1) * 0.70).astype(int)
axins.imshow(brain_slice[y1:y2, x1:x2], extent=(x1, x2, y1, y2), cmap=brain_cmap, origin="lower");
axins.set_xlim(x1, x2)
axins.set_ylim(y1, y2)
axins.set_xticklabels([])
axins.set_yticklabels([])
ax.indicate_inset_zoom(axins, edgecolor="black", alpha=1, linewidth=1.5);
if grid:
params = {}
if voxel_centers_c is not None:
params["norm"] = mpl.colors.CenteredNorm()
params["c"] = voxel_centers_c
params["cmap"] = "seismic"
elif voxel_centers_c is None:
params['c'] = 'black'
# Voxel centers
ax.scatter(*get_centers(brain_slice), s=10, **params)
axins.scatter(*get_centers(brain_slice), s=80, **params)
# Voxel edges
e_i = np.arange(0, z_slice.shape[1], step=12).astype(int)
e_j = np.arange(0, z_slice.shape[0], step=12).astype(int)
# Plot grid
ax.plot([e_i[1:-1]] * len(e_j), e_j, c='k', lw=1, alpha=0.3);
ax.plot(e_i, [e_j[1:-1]] * len(e_i), c='k', lw=1, alpha=0.3);
axins.plot([e_i[1:-1]] * len(e_j), e_j, c='k', lw=1, alpha=0.3);
axins.plot(e_i, [e_j[1:-1]] * len(e_i), c='k', lw=1, alpha=0.3);
return fig, ax, axins
def axis_cbar(ax):
cbar = inset_axes(
ax,
width="100%",
height="10%",
bbox_to_anchor=(0, -0.15, 1, 0.5),
bbox_transform=ax.transAxes,
loc='lower center',
)
cbar.set_aspect("auto")
return cbar
Data: a brain¶
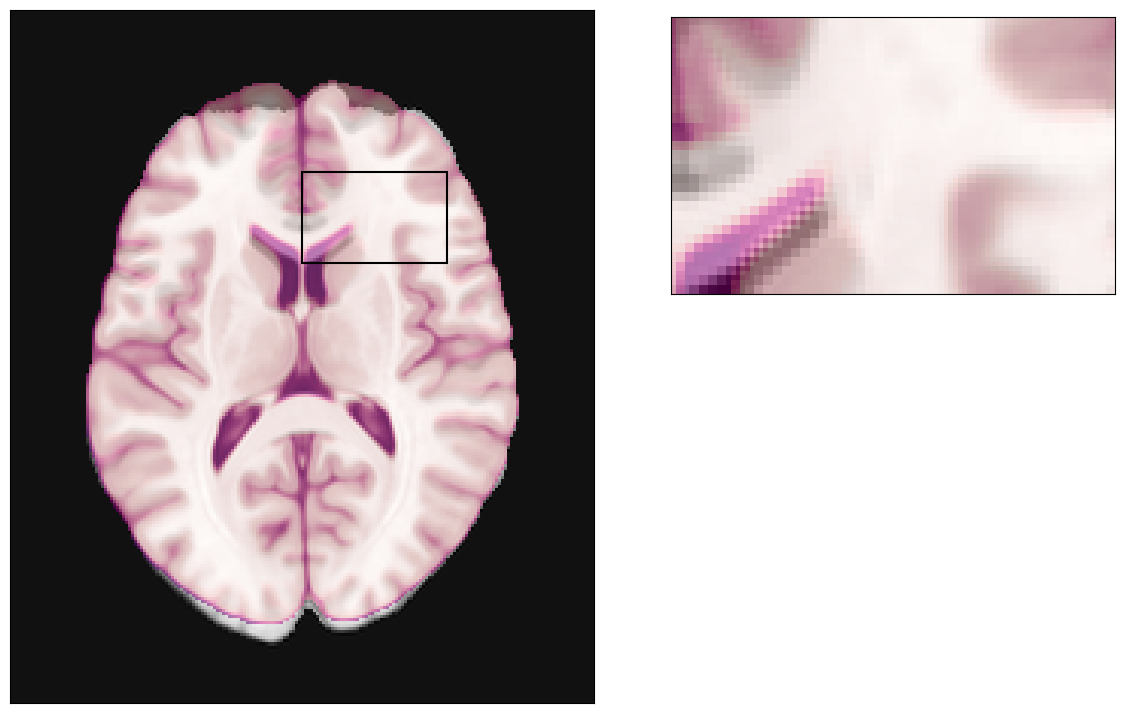
Let’s start getting some brain image model to work with, select a particular axial slice at the middle of it and visualize it.
[5]:
data = np.asanyarray(nb.load(get("MNI152NLin2009cAsym", desc="brain", resolution=1, suffix="T1w")).dataobj);
[6]:
z_slice = np.swapaxes(data[..., 90], 0, 1).astype("float32")
z_s = z_slice.copy()
z_slice[z_slice == 0] = np.nan
[7]:
plot_brain(z_slice);
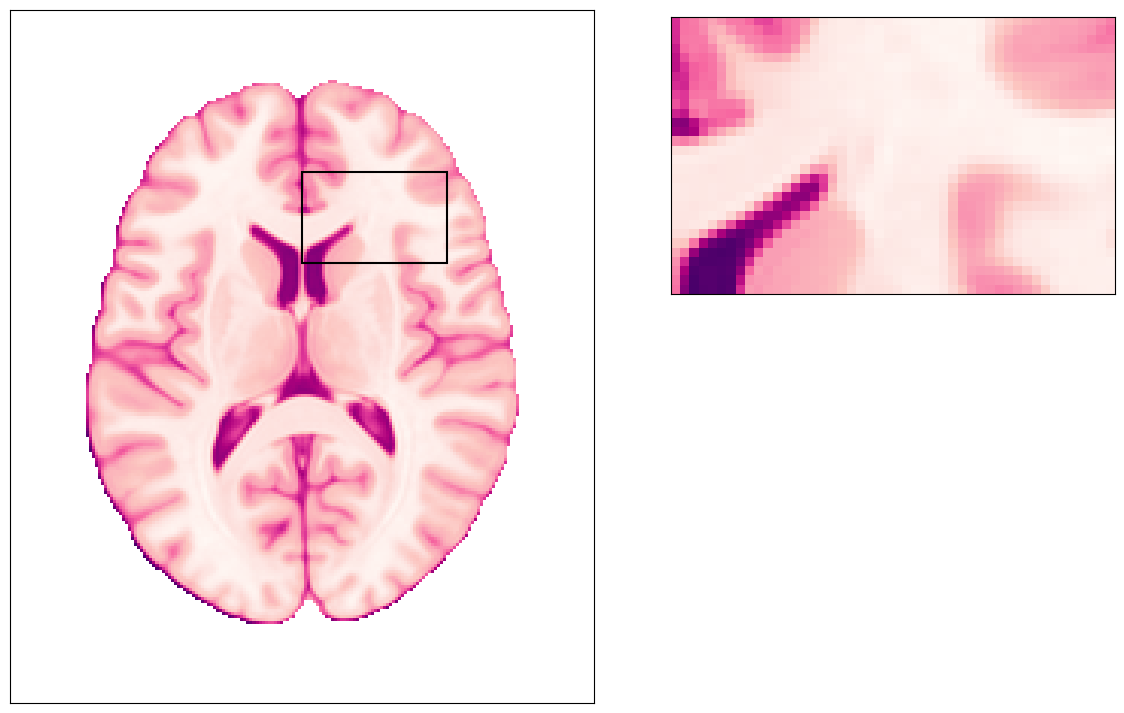
Sampling that brain and MRI¶
MRI will basically define an extent of phyisical space inside the scanner bore that will be imaged (field-of-view, Fov). That continuous space will be discretized into a number of voxels, and the signal corresponding to each voxel (a voxel is a volume element) will be measured at the center of the voxel (blue dots in the picture).
[8]:
plot_brain(np.ones_like(z_slice) * np.nan, grid=True);
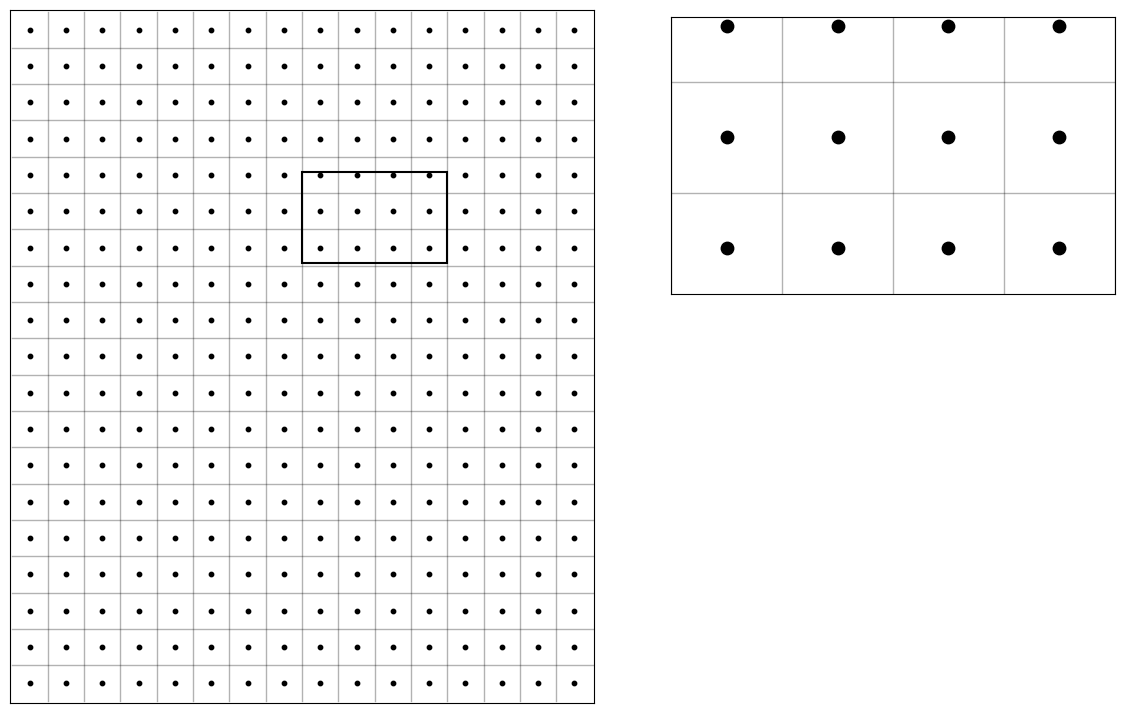
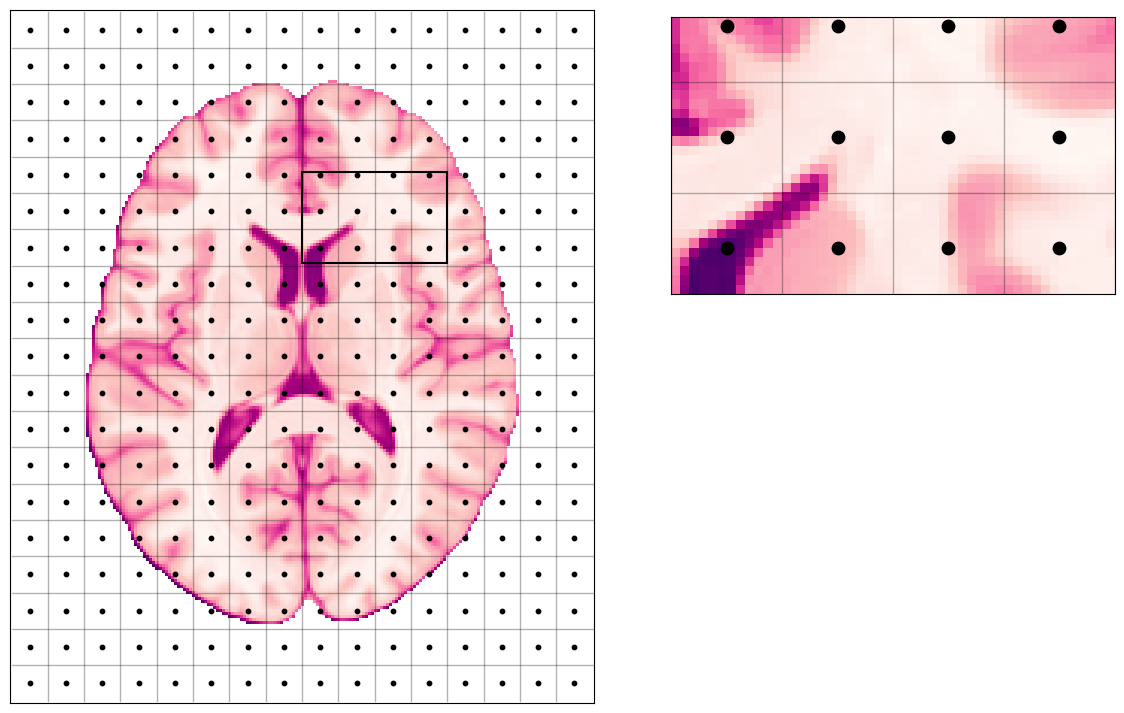
Which means, this discretization of the space inside the scanner will be imposed on the imaged object (a brain in our case):
[9]:
plot_brain(z_slice, grid=True);
The \(B_\text{0}\) field is not absolutely uniform¶
Indeed, inserting an object in the scanner bore perturbs the nominal \(B_\text{0}\) field, which should be constant all across the FoV (e.g., 3.0 T in all the voxels above, if your scanner is 3T).
In particular, some specific locations where the air filling the empty space around us is close to tissues, these deviations from the nominal \(B_\text{0}\) are larger.
[10]:
field = nb.load("fieldmap.nii.gz").get_fdata(dtype="float32")
[11]:
fig, ax, axins = plot_brain(z_slice, grid=True)
ax.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.4);
axins.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.4);
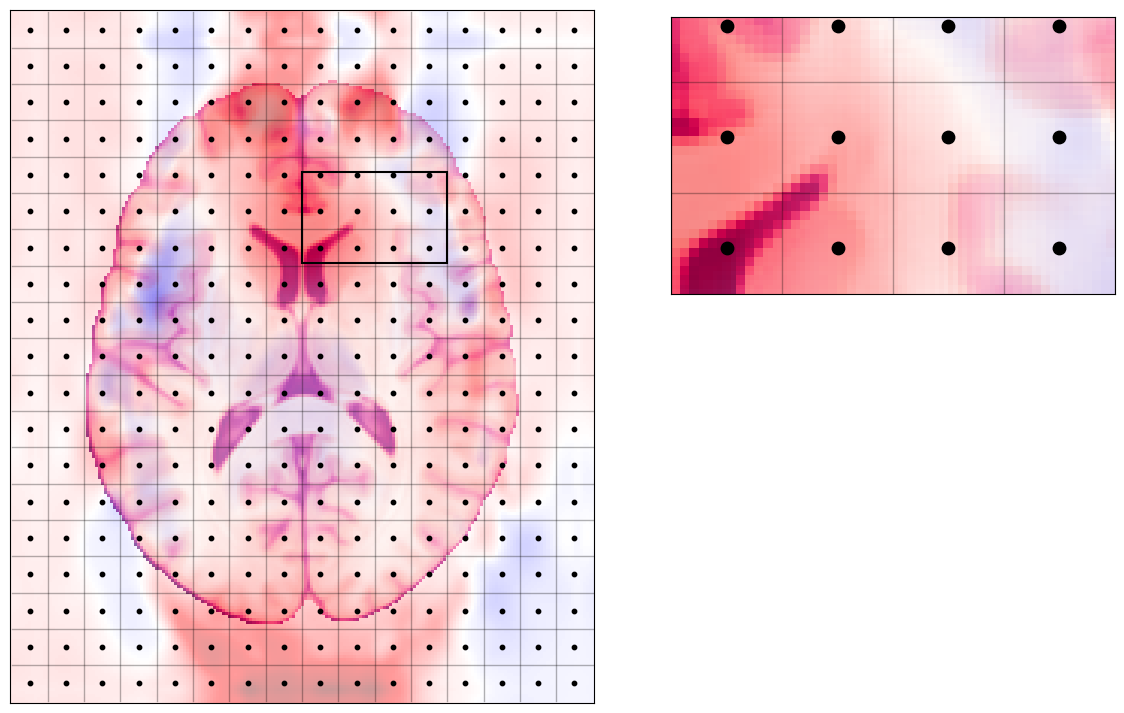
Then, we can measure (in reality, approximate or estimate) how much off each voxel of our grid deviates from the nominal field strength.
[12]:
x_coord, y_coord = get_centers(z_slice)
sampled_field = field[y_coord, x_coord]
[13]:
fig, ax, axins = plot_brain(np.ones_like(z_slice) * np.nan, grid=True, voxel_centers_c=sampled_field)
im = ax.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
axins.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
fig.colorbar(
im,
cax=axis_cbar(axins),
orientation='horizontal',
ticks=[-field.max(), 0, field.max()]
).set_ticklabels(
[r'$\Delta B_0 < 0$', r'$\Delta B_0 = 0$', r'$\Delta B_0 > 0$'],
fontsize=16,
)
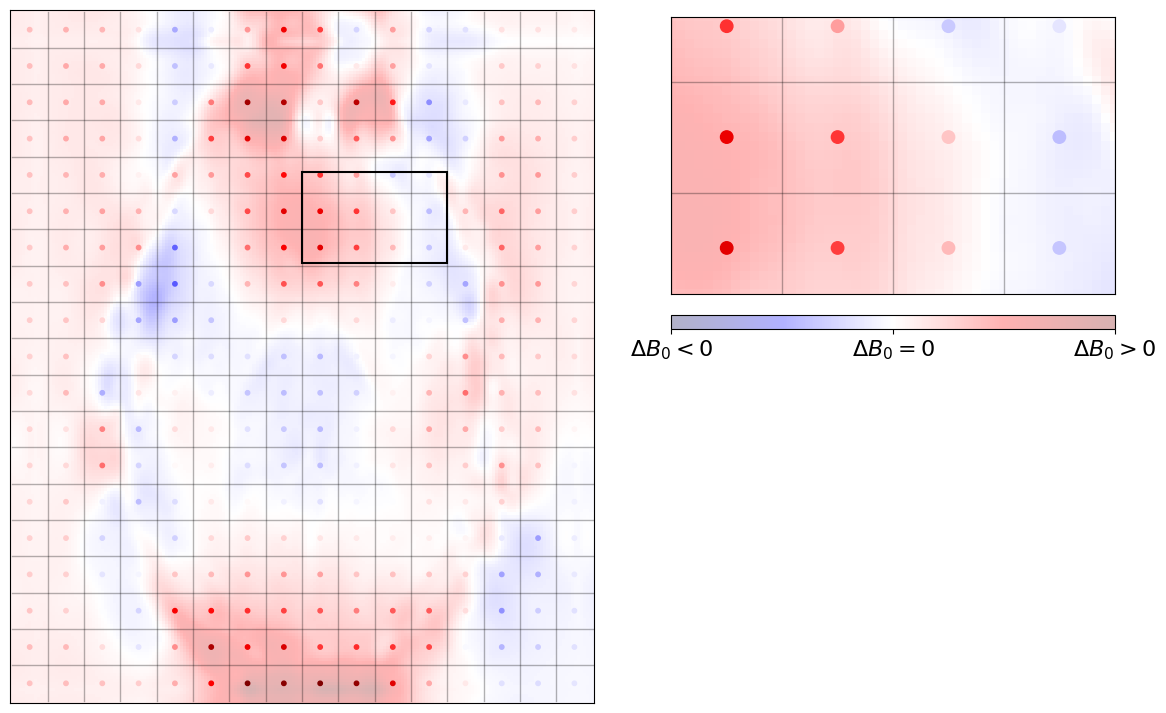
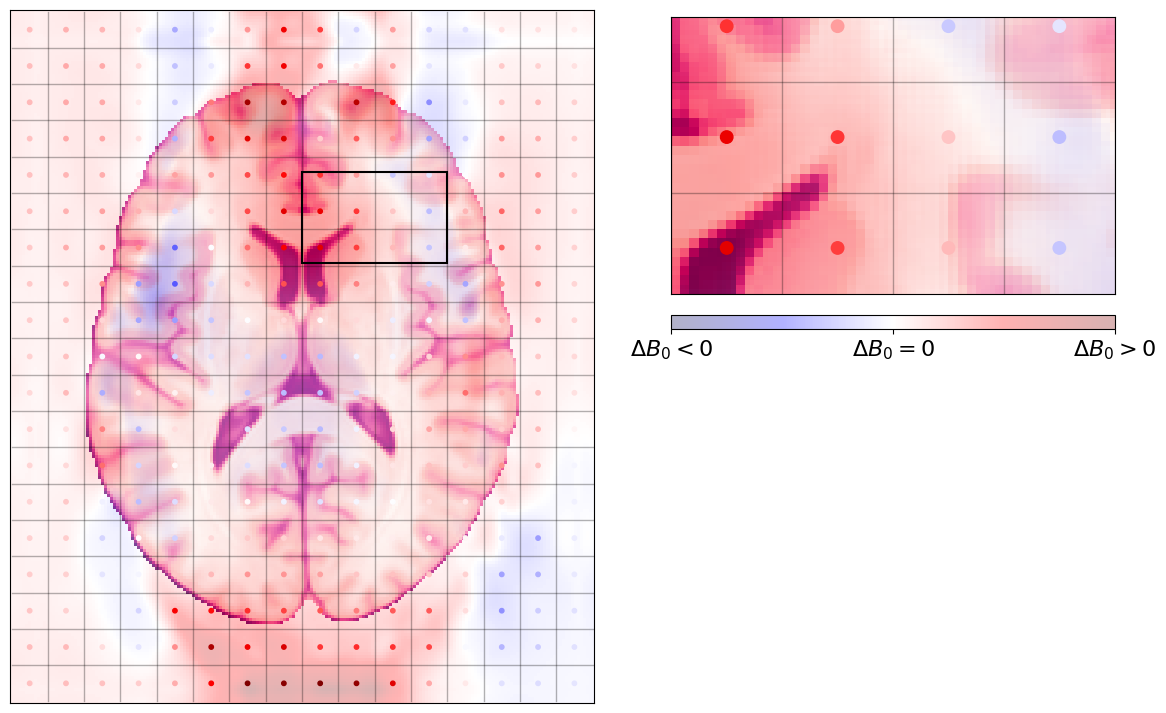
Those sampled deviations from the nominal field (\(\Delta B_\text{0}\)) can be plotted on top of our brain slice, to see where voxels are fairly close to their nominal value (e.g., those two white dots in the ventricles at the middle) and those furtherr from it (e.g., two voxels towards the anterior commissure which are very reddish).
[14]:
fig, ax, axins = plot_brain(z_slice, grid=True, voxel_centers_c=sampled_field)
im = ax.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
axins.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
fig.colorbar(
im,
cax=axis_cbar(axins),
orientation='horizontal',
ticks=[-field.max(), 0, field.max()]
).set_ticklabels(
[r'$\Delta B_0 < 0$', r'$\Delta B_0 = 0$', r'$\Delta B_0 > 0$'],
fontsize=16,
)
The second ingredient of the distortion cocktail - acquisition trade-offs¶
In addition to that issue, this problem becomes only apparent when some of the encoding directions has very limited bandwidth. Normally, anatomical images (MPRAGE, MP2RAGE, T2-SPACE, SPGR, etc.) have sufficient bandwidth in all encoding axes so that distortions are not appreciable.
However, echo-planar imaging (EPI) is designed to acquire extremelly fast - at the cost of reducing the bandwidth of the phase encoding direction.
When we have this limitation, the scanner will think it’s sampling at the regular grid above, but in turn, the signal will be coming from slightly displaced locations along the phase-encoding (PE) axis, that is, the encoding axis with lowest bandwidth (acquired fastest).
The formulae governing this distortion are described in the SDCFlows documentation.
[15]:
trt = - 0.15 # in seconds
[16]:
fig, ax, axins = plot_brain(z_slice, grid=True, voxel_centers_c=sampled_field)
# Voxel edges
e_i = np.arange(0, z_slice.shape[1], step=12).astype(int)
e_j = np.arange(0, z_slice.shape[0], step=12).astype(int)
# Actual sampling locations
y_coord_moved = y_coord + trt * sampled_field
# Whether actual sample locations fall within the image extents
is_in_fov = (y_coord_moved > 0) & (y_coord_moved < field.shape[0] - 1)
# Calculate quivers (vectors)
u = np.zeros(len(np.array(x_coord)[is_in_fov]))
v = y_coord_moved[is_in_fov] - np.array(y_coord)[is_in_fov]
c = -1.0 * v / np.abs(v).max()
# Main view's plotting
ax.quiver(
np.array(x_coord)[is_in_fov],
np.array(y_coord)[is_in_fov],
u,
v,
color='k',
# cmap='seismic',
angles='xy',
scale_units='xy',
scale=1,
)
im = ax.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
# Inset plotting
q = axins.quiver(
np.array(x_coord)[is_in_fov],
np.array(y_coord)[is_in_fov],
u,
v,
color='k',
# cmap='seismic',
angles='xy',
scale_units='xy',
width=0.008,
scale=1,
)
axins.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
fig.colorbar(
im,
cax=axis_cbar(axins),
orientation='horizontal',
ticks=[-field.max(), 0, field.max()],
).set_ticklabels([r'$s_{min}$', '0.0' , r'$s_{max}$'], fontsize=16)
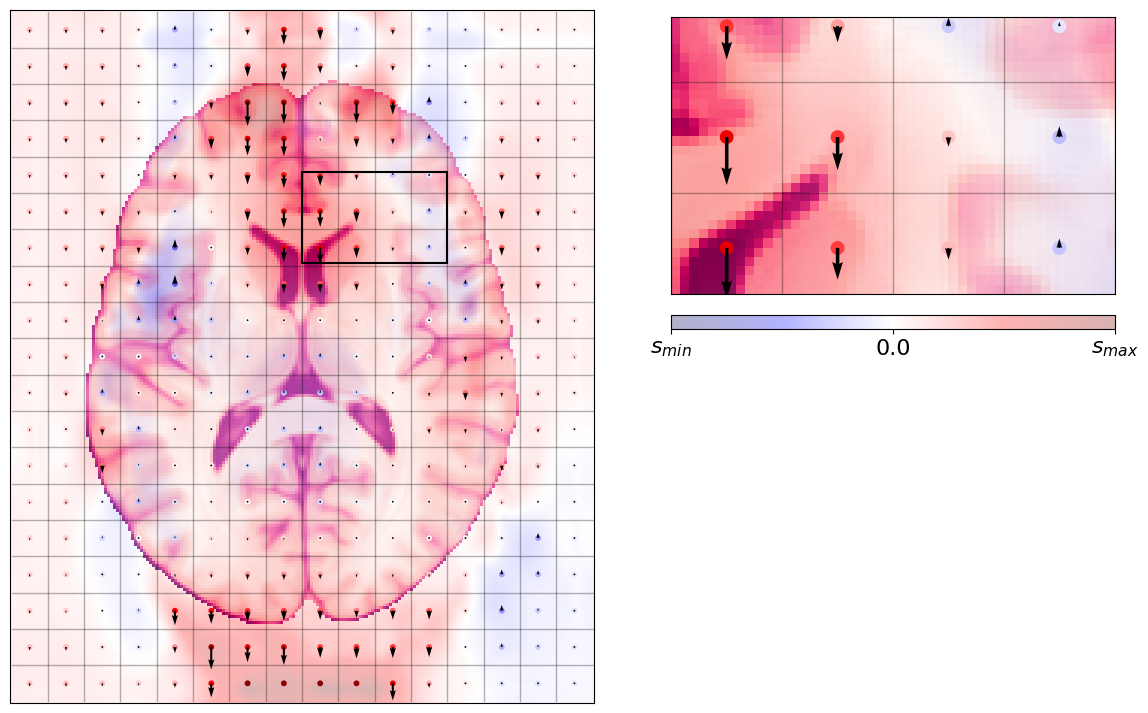
[17]:
fig, ax, axins = plot_brain(z_slice, grid=False)
# Calculate quivers (vectors)
u = np.zeros(len(np.array(x_coord)[is_in_fov]))
v = y_coord_moved[is_in_fov] - np.array(y_coord)[is_in_fov]
c = -1.0 * v / np.abs(v).max()
# Plot main view
ax.scatter(np.array(x_coord)[is_in_fov], np.array(y_coord)[is_in_fov], s=10, c='k')
ax.scatter(np.array(x_coord)[is_in_fov], y_coord_moved[is_in_fov], c=c, s=10, cmap="seismic", vmin=-1, vmax=1)
ax.plot([e_i[1:-1]] * len(e_j), e_j, c='k', lw=1, alpha=0.3);
im = ax.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
# Plot inset
axins.scatter(np.array(x_coord)[is_in_fov], np.array(y_coord)[is_in_fov], s=80, c=None, fc='none', ec='k')
axins.scatter(np.array(x_coord)[is_in_fov], y_coord_moved[is_in_fov], s=80, c=c, cmap='seismic', vmin=-1, vmax=1)
axins.quiver(
np.array(x_coord)[is_in_fov],
y_coord_moved[is_in_fov],
u,
-v,
color="black",
angles='xy',
scale_units='xy',
width=0.008,
scale=1,
)
axins.plot([e_i[1:-1]] * len(e_j), e_j, c='k', lw=1, alpha=0.3);
axins.imshow(field, cmap="seismic", norm=mpl.colors.CenteredNorm(), origin="lower", alpha=0.3);
# Calculate warping
j_axis = np.arange(z_slice.shape[1], dtype=int)
for i in e_j:
warped_edges = i + trt * field[i, :]
warped_edges[warped_edges <= 0] = np.nan
warped_edges[warped_edges >= field.shape[0] - 1] = np.nan
ax.plot(j_axis, warped_edges, c='k', lw=1, alpha=0.5);
axins.plot(j_axis, warped_edges, c='k', lw=1, alpha=0.5);
fig.colorbar(
im,
cax=axis_cbar(axins),
orientation='horizontal',
ticks=[-field.max(), 0, field.max()],
).set_ticklabels([r'$s_{min}$', '0.0', r'$s_{max}$'], fontsize=16)
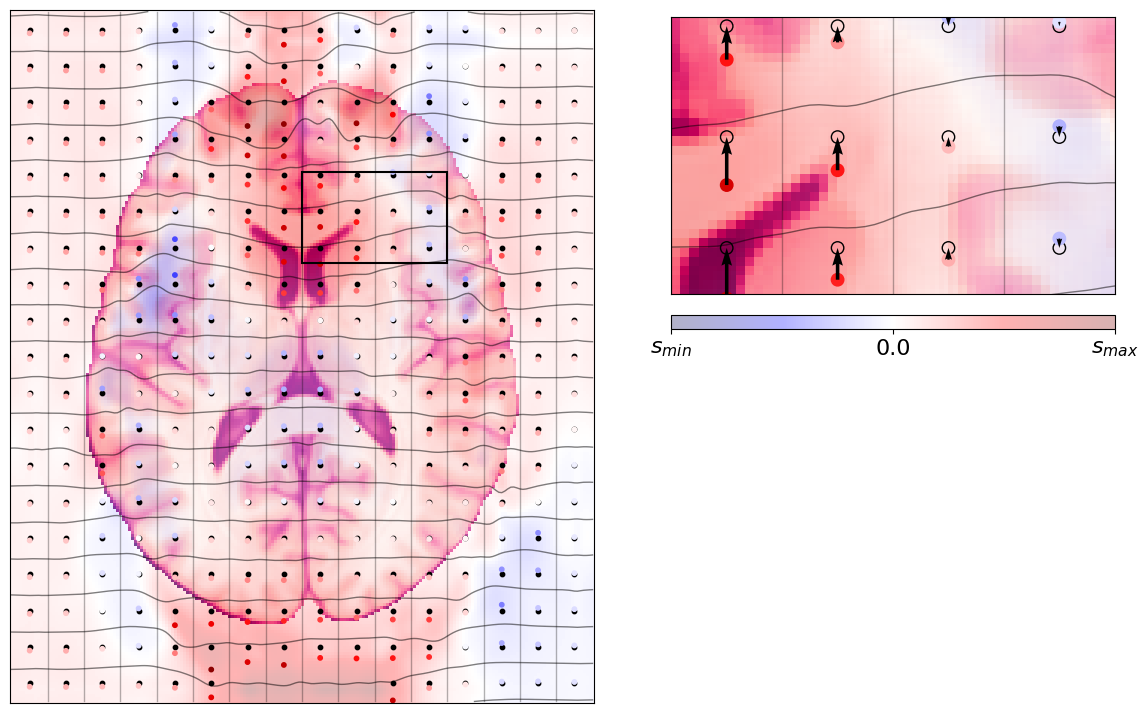
The effects of this physical phenomenon¶
Then the MRI device will execute the EPI scanning scheme, and sample at the locations given above. The result can be seen in the image below:
[18]:
all_indexes = tuple([np.arange(s) for s in z_slice.shape])
all_ndindex = np.array(np.meshgrid(*all_indexes, indexing="ij")).reshape(2, -1)
[19]:
all_ndindex_warped = all_ndindex.astype("float32")
all_ndindex_warped[0, :] += trt * field.reshape(-1)
[20]:
warped_brain = ndi.map_coordinates(
z_s,
all_ndindex_warped,
).reshape(z_slice.shape)
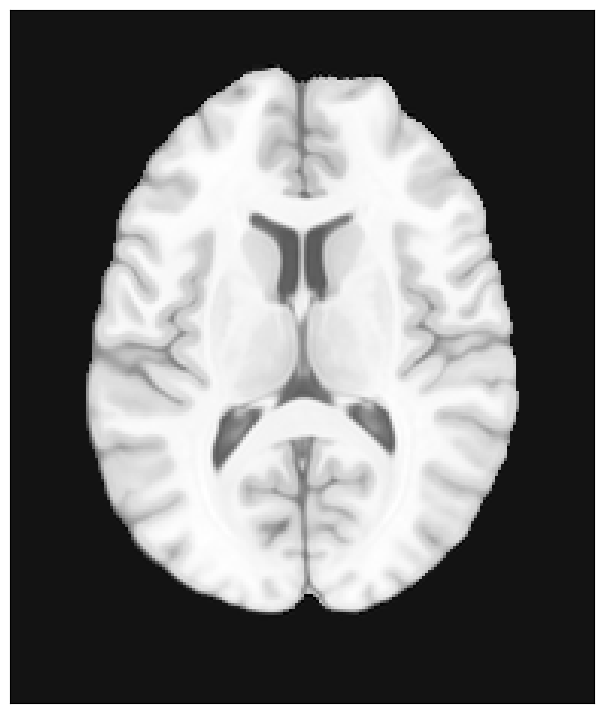
[21]:
plot_brain(warped_brain, grid=True, brain_cmap='gray');
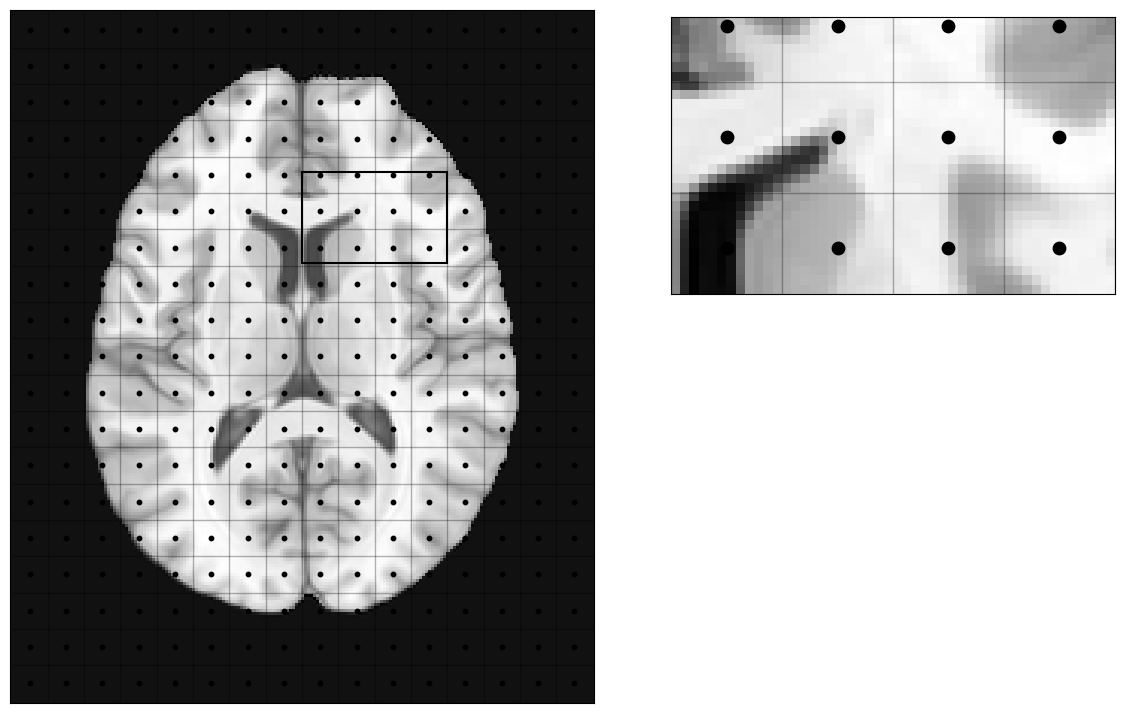
For reference, we can plot our MRI (grayscale colormap) fused with the original (ground-truth) anatomy.
[22]:
fig, ax, axins = plot_brain(warped_brain, grid=False, brain_cmap='gray');
im = ax.imshow(z_slice, cmap="RdPu_r", origin="lower", alpha=0.5);
axins.imshow(z_slice, cmap="RdPu_r", origin="lower", alpha=0.5);
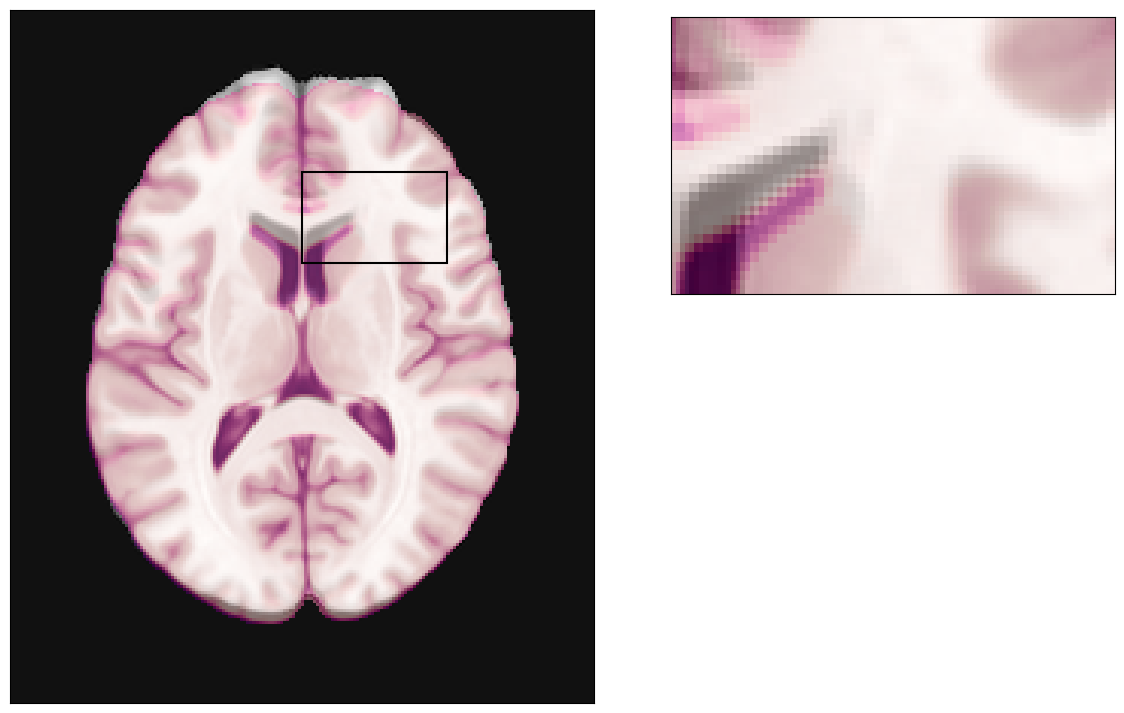
The effect if the PE direction is reversed (“negative blips”)¶
Then, the distortion happens exactly on the opposed direction:
[23]:
all_ndindex_warped = all_ndindex.astype("float32")
all_ndindex_warped[0, :] -= trt * field.reshape(-1)
warped_brain = ndi.map_coordinates(
z_s,
all_ndindex_warped,
).reshape(z_slice.shape)
fig, ax, axins = plot_brain(warped_brain, grid=False, brain_cmap='gray');
im = ax.imshow(z_slice, cmap="RdPu_r", origin="lower", alpha=0.5);
axins.imshow(z_slice, cmap="RdPu_r", origin="lower", alpha=0.5);